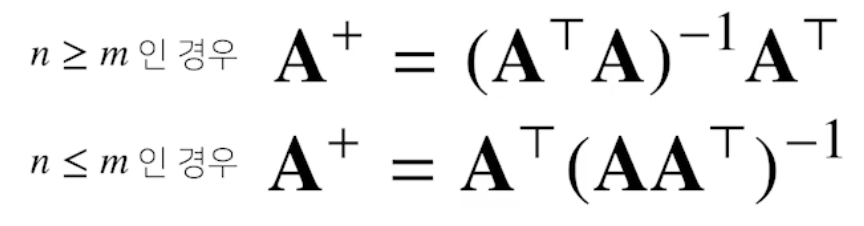행렬이 뭐에요?

행렬이란?

• 행렬은 벡터를 원소로 가지는 2차원 배열
• 행렬은 행과 열이라는 인덱스를 가진다.
• 행렬의 특정 행(열)을 고정하면 행(열)벡터라고 부른다.
• 전치행렬(transpose matrix)은 행과 열의 인덱스가 바뀐 행렬이다.
• 벡터가 공간에서 한 점이었다면, 행렬은 여러 점을 나타낸다.
• 행렬끼리 같은 모양을 가지면 덧셈, 뺄셈, 성분곱을 계산할 수 있다.
• 행렬곱은 i번째 행벡터와 j번째 열벡터 사이의 내적을 성분으로 가지는 행렬을 계산한다.
• 행렬은 벡터공간에서 사용되는 연산자(operator)로 이해한다.
• 행렬곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있다.
• 행렬곱을 통해 패턴을 추출할 수 있고, 데이터를 압축할 수도 있다.
• 모든 선형변환(linear transform)은 행렬곱으로 계산할 수 있다.

역행렬

• 어떤 행렬 A의 연산을 거꾸로 되돌린 행렬을 역행렬이라 한다.
• 역행렬은 행과 열 숫자가 같고 행렬식(determinant)이 0이 아닌 경우에만 계산할 수 있다.
• 역행렬을 계산할 수 없다면 유사역행렬(pseudo-inverse) 또는 무어-펜로즈(Moore-Penrose)역행렬을 이용한다.
  • 
• 유사역행렬을 이용하면 데이터를 선형모델로 해석하는 선형회귀식을 찾을 수 있다.