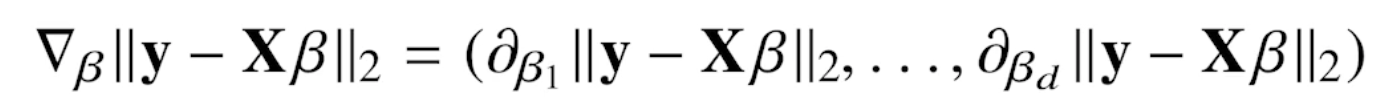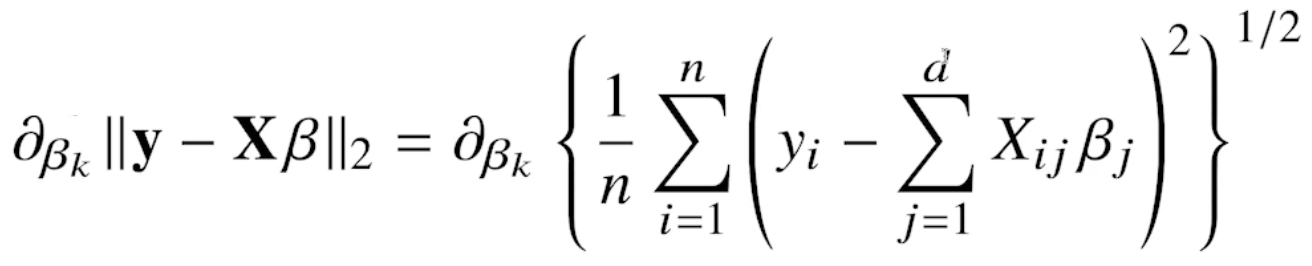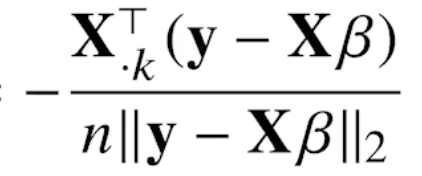경사하강법

미분

• 미분은 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구로 최적화에서 가장 많이 사용하는 기법이다.
• 미분은 함수 f의 주어진 점 (x, f(x))에서의 접선의 기울기를 구한다.
• 미분값을 더하면 경사상승법(gradient ascent)이라 하며, 함수의 극대값의 위치를 구할 때 사용한다.
• 미분값을 빼면 경사하강법(gradient descent)이라 하며, 함수의 극소값의 위치를 구할 때 사용한다.
• 경사상승/경사하강법은 극값에 도달하면 움직임을 멈춘다.

# gradient: 미분 계산 함수
# init: 시작점, lr: 학습률, eps: 알고리즘 종료조건

var = init
grad = gradient(var)
while(abs(grad) > eps):
	var = var - lr * grad
	grad = gradient(var)

• 미분은 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구로서, 최적화에서 제일 많이 사용하는 기법이다.
• 벡터가 입력인 다변수 함수의 경우 편미분(partial differentiation)을 사용한다.
• 각 변수 별로 편미분을 계산한 그래디언트 벡터(gradient vector)를 이용하여 경사하강/상승법에 사용할 수 있다.
  • Nabla(역삼각형) 기호로 표기

역행렬을 이용한 선형회귀분석

• np.linalg.pinv 를 이용하면 데이터를 선형모델로 해석하는 선형회귀식을 찾을 수 있다.

• 행렬 X(n, m)에서 n >= m인 경우,

  • XB = y_hat ~= y

    -> B = X^+ * y (L2-노름을 최소화)

    -> = (X^T X)^-1 X^T * y

• 선형모델의 경우 역행렬을 이용하여 회귀분석이 가능하다.

경사하강법을 이용한 선형회귀분석

• 선형회귀의 목적식은 ||y - XB||2 이고, 이를 최소화하는 B를 찾아야 하므로 아래와 같은 그래디언트 벡터를 구해야 한다.

  • 

  • 

  • 

• # norm: L2-노름을 계산하는 함수
  # lr: 학습률, T: 학습횟수
  
  for t in range(T):
      error = y - X @ beta
      grad = - transpose(X) @ error
      beta = beta - lr * grad
  

• 이론적으로 경사하강법은 미분가능하고 볼록(convex)한 함수에 대해선 적절한 학습률과 학습횟수를 선택했을 때 수렴이 보장되어 있다. (볼록한 함수는 그래디언트 벡터가 항상 최소점을 향하기 때문)

확률적 경사하강법(SGD, Stochastic Gradient Descent)

• 확률적 경사하강법은 모든 데이터가 아닌 데이터 한 개 또는 일부(mini batch)를 활용하여 업데이트한다.
• 볼록함수가 아닌(non-convex) 목적식은 SGD를 통해 최적화할 수 있다.
• SGD는 데이터의 일부를 가지고 파라미터를 업데이트하기 때문에 연산자원을 좀 더 효율적으로 활용하는데 도움이 된다.
  • 전체 데이터(X, y)를 쓰지 않고 미니배치(X(b), y(b))를 사용하여 업데이트하므로 연산량이 b / n 으로 감소한다.