Semantic Segmentation

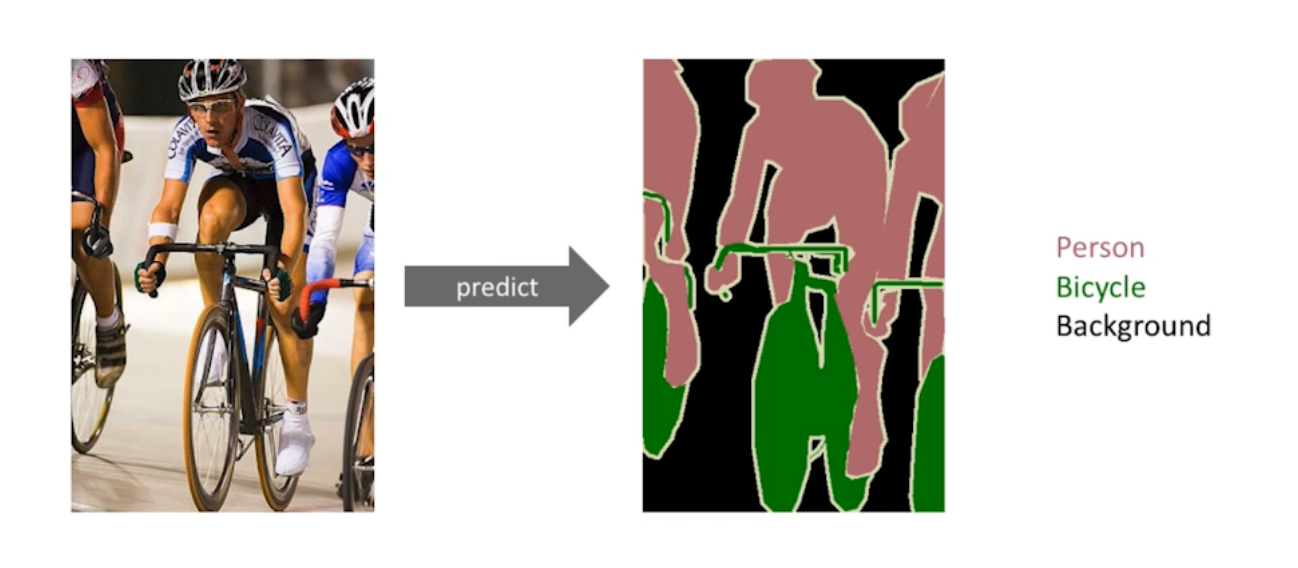
이미지 픽셀 별 분류 과제이다. Dense Classification, Perl Pixel 등으로 불리기도 한다.

• Fully Convolutional Network

  • output이 1000개의 채널이라고 하면, Dense Layer를 없애고 Fully Convolutional Network 로 변경하려는 것임.

  • Fully Connected (Dense) Layer를 사용하는 것과 결과적으로 똑같음. 파라미터도 완전히 똑같음.

    

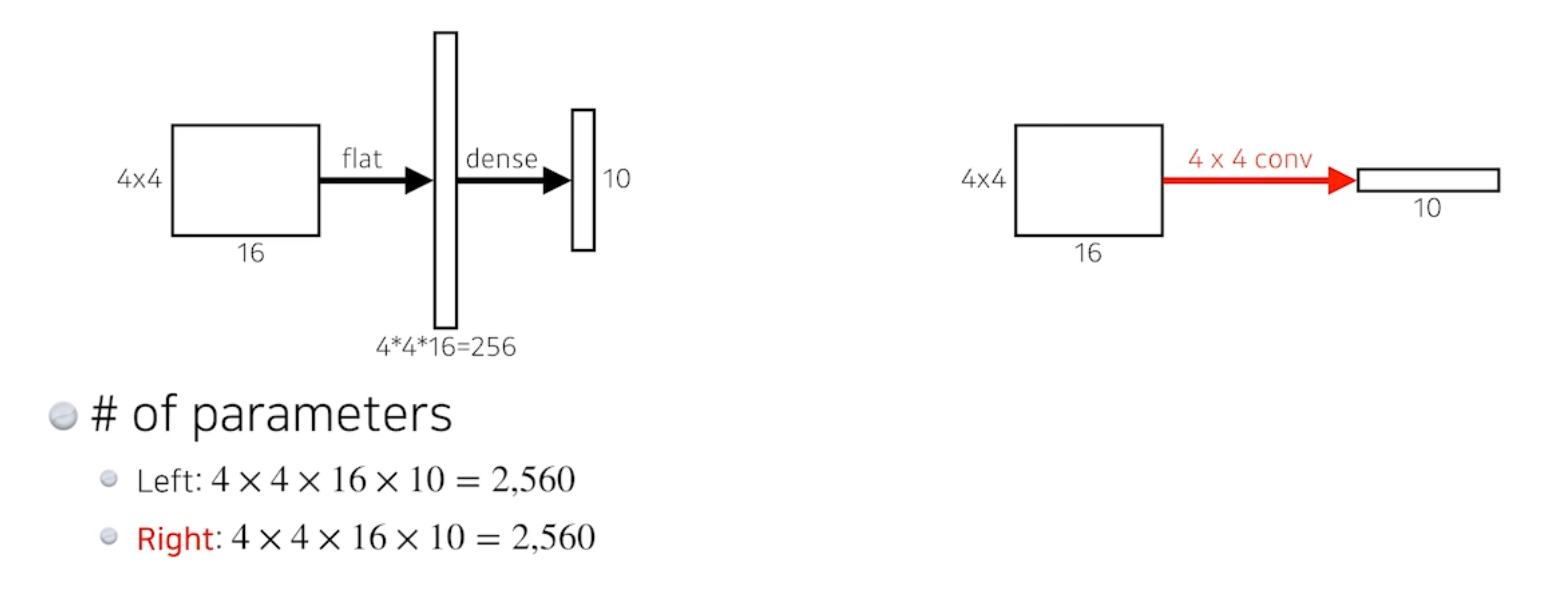
  • 이러한 과정을 convolutionalization 이라고 한다.

    • Transforming fully connected layers into convolution layers enables a classification net to output a heat map.

  • While FCN can run with inputs of any size, the output dimensions(special dimension) are typically reduced by subsampling. So we need a way to connect the coarse output to the dense pixels.

• Deconvolution (conv transpose)

  • 직관적으로 보았을 때 Convolution의 역 연산이다.

    

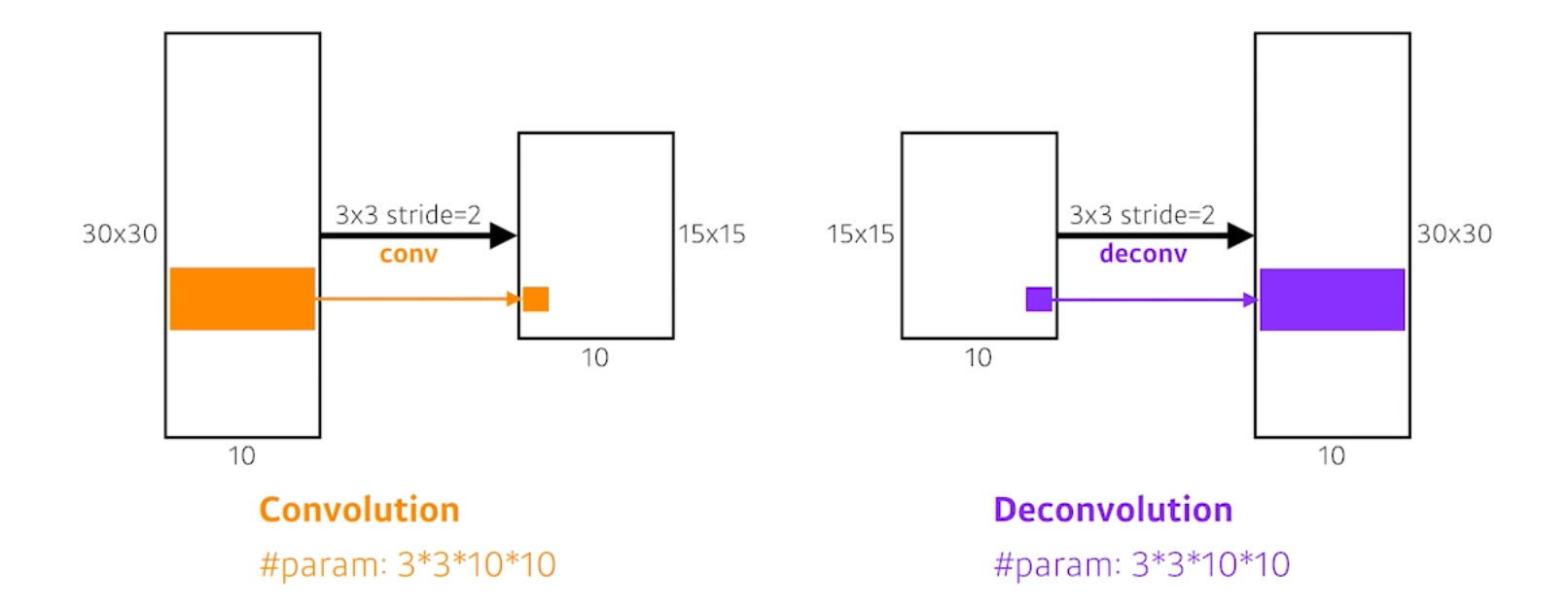
  • special dimension을 키워주는 역할을 하게 된다.

  • 엄밀히 말하면 convolution의 역 연산은 존재할 수 없다. 원래의 값으로 완전히 복원할 수는 없기 때문이다. 하지만 이렇게 생각하면 좋은 이유는 네트워크 구조를 짤 때 파라미터 크기와 네트워크 입출력을 계산할 때 역으로 생각하면 편하기 때문이다.

Detection

Semantic Segmentation 이랑 비슷하지만, 퓨어픽셀을 이용한 히트맵을 찾는 것이 아니라 객체들의 bounding box를 찾는 과제로 만든 것이다.

• R-CNN
  1. R-CNN takes an input image,
  2. extracts around 2,000 region proposals (using Selective search),
  3. compute features for each proposal (using AlexNet),
  4. and then classifies with lenear SVMs.
• SPPNet
  • RCNN의 가장 큰 문제는 이미지에서 2000개의 바운딩박스를 뽑았을 때, 2000개의 이미지 혹은 패치를 모두 CNN에 통과시켜야 한다. 즉 하나의 이미지를 처리하는데 CPU에서는 1분의 시간이 소요되었었다.
  • 이미지 전체에 대한 컨볼루션 피쳐맵을 만들고, 뽑힌 바운딩박스 위치에 해당하는 컨볼루션 피쳐맵의 텐서만 뽑아온 것으로 CNN에 통과시킴으로써 훨씬 빨라지며, 한 번의 CNN으로 결과를 얻을 수 있다.
• Fast R-CNN
  • 
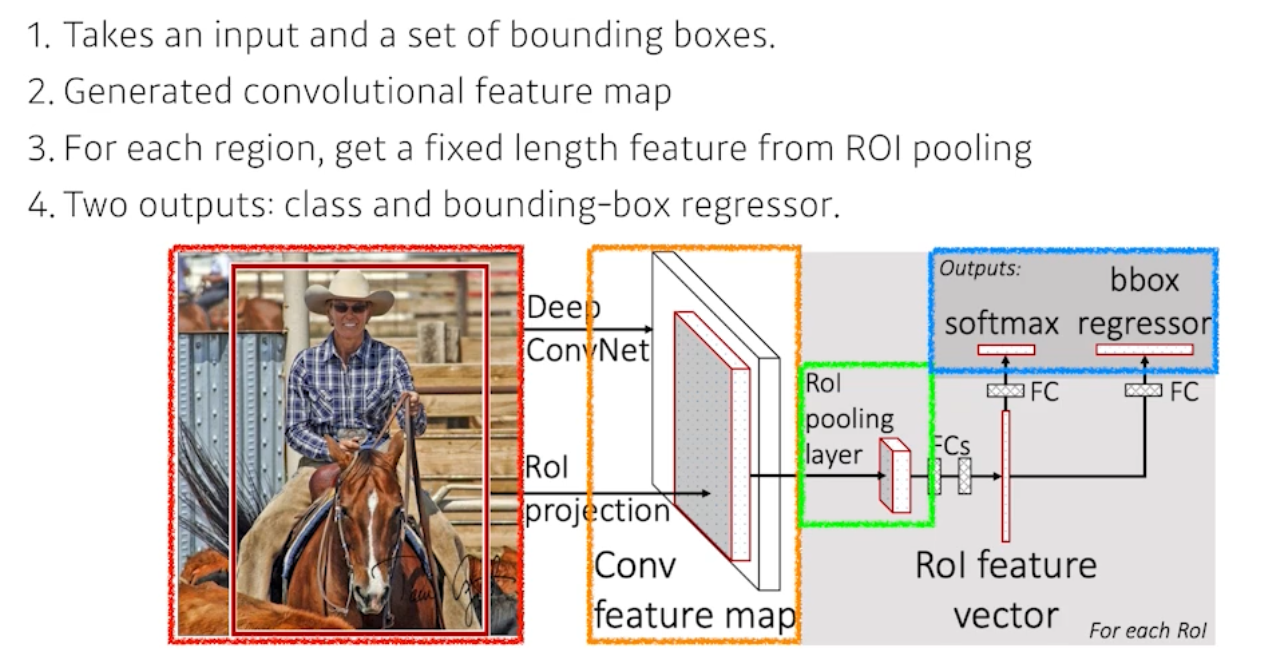
  • 기본 컨셉은 SPPNet과 굉장히 유사하지만, 뒷단의 Neural Net(RoI)을 통해서 바운딩박스 리그레션과 분류를 진행했다.
• Faster R-CNN
  • 이미지를 통해 바운딩박스를 뽑아내는 Region Proposal 역시 학습을 시키자는 것임.
  • 
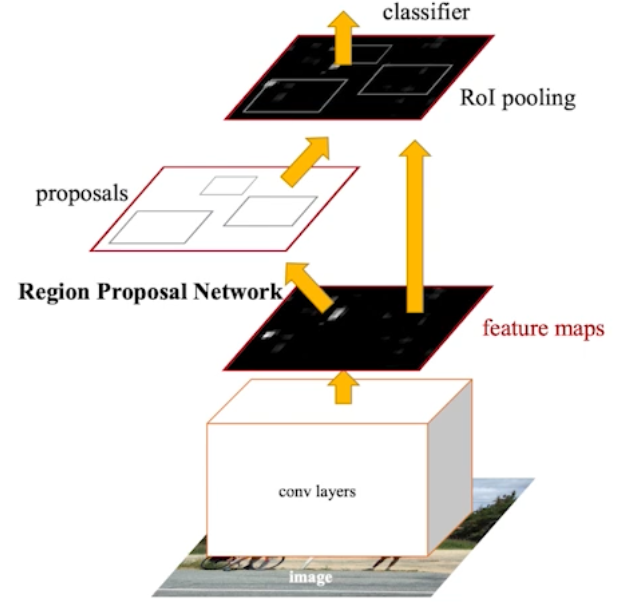
  • Region Proposal Network
    • 이미지가 있으면 이미지 속 특정 영역(패치)이 바운딩박스로서 의미가 있는지 없는지(즉 영역에 물체가 있는지)를 판단하는 것이다.
    • anchor boxes가 필요한데, 이것은 미리 정해놓은 바운딩박스의 크기이다. 내가 이 영역에 어떤 크기의 물체가 있을 것 같다라는 예상을 전제로 만들어 놓은 것임.
    • Fully Conv 레이어가 사용됨.
  • YOLO
    • extremely fast object detection algorithm
    • It simultaneously predicts multiple bounding boxes and class probabilities.
      • No explicit bounding box sampling (compared with Faster R-CNN)
    • 
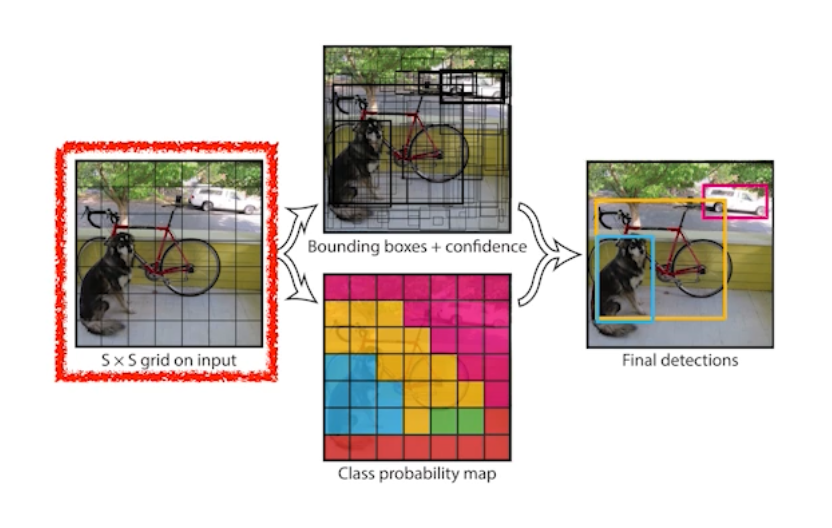
      • 이미지 안에 찾고싶은 물체의 중앙이 그리드 안에 들어가면, 그 그리드 셋이 해당 물체의 바운딩 박스와 해당 물체가 무엇인지 같이 예측을 해야 한다.
      • 이 때 B개의 바운딩 박스를 예측하게 된다. 이후 바운딩박스의 refinement(x/y/w/h)를 예측하고, 각각의 그리드셋이 속하는 중점의 오브젝트가 어떤 클래스인지 예측한다.
      • 이 두 가지 정보를 취합하게 되면 박스와 박스가 어떤 클래스인지 예측할 수 있다.

파라미터 수 손으로 직접 계산해보기

알렉스넷의 파라미터 수 구하기

input = 224 224 3
filter = 11 11 3
fisrt param = $11113482 ~= 35k$

Modern CNN

AlexNet

네트워크가 두 개로 나뉘어져 있다. 당시 GPU가 부족했기 때문임. 두 장의 GPU로 학습하고 합쳤다. 인풋에 $11 * 11$ 필터를 사용했는데, 파라미터 관점에서 좋진 않다. 상대적으로 많은 파라미터가 필요하기 때문. 이후 5개의 Convolution 레이어와 3개의 Dense 레이어를 사용한다. 최근 200-300개 네트워크를 가진 신경망에 비하면 Light한 편이다.

Key Ideas

• Rectified Linear Unit(ReLU) 활성화 함수를 사용했다. $ReLU = max(0, x)$
  • 리니어 모델이 갖는 좋은 성질들을 가질 수 있게 한다.
  • 리니어 모델들의 성질을 가지고 있기 때문에 학습하는 SGD나 Gradient Descent로 학습을 용이하게 한다.
  • 활성화함수를 사용할 때 이전에 많이 활용하던 Sigmoid나 tanh 같은 경우 값이 커지면 슬로프가 줄어들게 된다. 슬로프가 결국 기울기니까, 뉴런의 값이 많이 크면(0에서 벗어나면) Gradient Slope는 0에 가까워진다. 이 때 Vanishing Gradient 문제가 발생할 수 있는데, ReLU를 사용하면 해당 문제를 해소할 수 있음
• GPU Implementation (2 GPUs)
• Local Response Normalization(어떠한 입력 공간에서 Response가 많이 나오는 부분을 죽이는 것임. 최근엔 많이 사용되지 않음), Overlapping pooling
• Data Augmentation
• Dropout

“Language is the source of misunderstandings” - Antoine de Saint-Exupery (1900-1944)

용어에 대한 정리를 하고 넘어가야 이후에 오해가 생기지 않는다. 용어 통일이 가장 중요하기 때문에 용어에 대한 명확한 컨셉을 잡아볼 것임.

Introduction

Gradient Descent

• First-order iterative optimization algorithm for finding a local minimum of a differentiable function.
• 찾고자 하는 파라미터에 대해서 손실함수를 미분한 편미분값을 가지고 학습을 하겠다는 것임.
• Local minimum: 손실함수를 미분했을 때 극소적으로 좋은 로컬 미니멈을 찾는 것을 목적으로 함.

Important Concepts in Optimization

• Generalization (일반화)

  • 대부분의 경우 일반화 성능을 높이는 것이 목적이다.
  • 일반화 성능을 높이기만 하면 좋은 것인가?
    • 일반적으로 학습을 시키게 되면 Iteration이 지나면서 Training Error를 줄이게 되는데, Training Error가 0이 되었다고 해서 우리가 항상 원하는 최적값에 도달했다는 보장이 없다.
    • 일반적으로 Training error가 주어지지만, 어느정도 시간이 지나고 나면 Test Error가 커짐, 즉 학습에 사용하지 않은 데이터에 대해서는 성능이 오히려 떨어지게 된다.
    • 즉, 일반적으로 일반화는 테스트에러와 트레이닝 에러의 갭을 줄이는 것을 의미한다.
    • 만약 우리 네트워크가 안좋아서 학습데이터에 대한 성능이 안좋으면, 일반화의 퍼포먼스가 좋다고 해서 테스트 데이터의 성능이 좋다고 말할 수 없다.
    • 일반화의 성능은 테스트와 트레이닝 에러의 갭을 말하기 때문이다.

• Under-fitting vs. over-fitting

  • 학습데이터에 대해서는 잘 동작을 하지만 테스트데이터에 대해서 잘 동작하지 않는 것을 OverFitting이라고 한다.

    

• Cross validation

  • 일반적으로 데이터가 분리되어 있음 (Train, Test, Validate)
  • 보통은 학습 데이터로 학습시킨 모델이 학습에 사용되지 않은 밸리데이션 데이터를 기준으로 학습이 잘 되었는지 확인하는 과정이다.
  • 하지만, 트레인과 테스트를 반반으로 했을 때, 트레인을 80 테스트를 20으로 했을 때 등 Split 범위에 따라서 학습의 퍼포먼스가 달라질 수 있다. 이러한 것을 해결하고자 하는 것이 Cross Validation이다. (혹은 K-Fold Validation)
  • 네트워크를 학습할 때 수많은 파라미터가 존재한다. 또한 Hyper Parameter들에 대한 기준이 없다. 따라서 Cross-validation을 통해 최적의 Parameter Sets 을 찾고, 파라미터를 보정한 상태에서 모든 학습데이터를 학습에 사용해야 더 많은 데이터를 사용할 수 있다.
  • Test Data는 어떠한 방법으로든 학습에 사용되어서는 안된다. 즉, 학습에는 Train과 Validate 데이터만을 이용해야 한다.

• Bias-variance tradeoff

  • 

  • 사격을 할 때 항상 같은 곳에만 찍히면 (원점이 아니더라도) 좋은 것이다. 전체 모델을 어느정도 평준화 시키면 최적값에 도달할 가능성이 많기 때문이다. 이것을 Low Variance라고 한다. (출력이 얼마나 일관적으로 나오는 지)

  • 이것에 반해 Variance가 크면 비슷한 입력이 들어와도 출력이 많이 달라지는 것을 의미한다.

  • Bias라는 것은 출력에 따른 평균적으로 True Target에 접근하는 정도를 의미하며, Bias가 크면 Mean에서 많이 벗어나는 것을 의미한다.

  • 학습 데이터에 Noise가 껴있다고 가정했을 때 내가 이 노이즈가 껴있는 타겟 데이터를 미니마이즈하는 것에 대하여 세 파트로 나뉘어진다. 내가 미니마이즈하는 것은 하나의 값(cost)이지만, 그 값은 세 파트로 나뉘어져 있어서 한 파트를 줄이면 다른 파트가 커질 수밖에 없는 Trade-off 관계이다.

    $$\begin{aligned} \mathbb{E}\left[(t-\hat{f})^{2}\right] &=\mathbb{E}\left[(t-f+f-\hat{f})^{2}\right] \\ &=\ldots \\ &=\mathbb{E}\left[\left(f-\mathbb{E}[\hat{f}]^{2}\right)^{2}\right]+\mathbb{E}\left[(\mathbb{E}[\hat{f}]-\hat{f})^{2}\right]+\mathbb{E}[\epsilon] \end{aligned}$$

    위 식에서 cost를 minimize한다는 것은 bias와 variance, noise를 minimize 한다는 것을 의미한다.

• Bootstrapping

  • 신발끈을 말하는 것이며, 그 뜻은 신발끈을 들어올려 하늘을 날겠다라는 허황된 뜻임.
  • 딥러닝에서는 학습 데이터가 100개가 있다고 하면, 100개 중 80개를 사용하겠다 등 일부만 뽑아서 사용한다는 것을 의미한다.
  • 이렇게 했을 때 하나의 입력에 대해서 각 모델들의 출력이 달라질 수 있다. 이 때 각 모델들의 예측값들이 얼마나 일치를 이루는지 보고 전체 모델들의 특성을 알고자 하는 것이다.
  • 학습데이터가 고정되어 있을 때 subsampling을 통해 여러 학습데이터를 만들고 그것을 이용하여 여러 모델 혹은 metric을 만들겠다는 것임.

• Baggin and boosting

  • Bagging(Bootstrapping aggregating)
  • 학습데이터를 여러 개를 만들어서 (Booststrapping) 여러 모델을 만들고 그 모델의 output들을 가지고 평균을 내겠다는 뜻임.
  • 학습데이터가 고정되어 있으면 이것을 모두 이용하여 하나의 결과를 내는 것이 좋을 것 같지만 사실은 그렇지 않다. N개의 모델을 만들고, N개의 모델의 출력값의 평균이나 Voting을 통해 나오는 결과를 사용하는 것이 보통 성능이 더 좋다.
  • Boosting: 학습데이터를 시퀀셜하게 바라봐서 간단한 모델을 만들고, 모델에 학습데이터를 다 넣어본다. 모델에서 80개는 잘 예측을 했지만 20개는 잘 안되었다. 이 때 모델을 하나를 더 만드는데 전에 안되었던 20개에 데이터를 잘 예측하는 모델을 만든다. 이렇게 모델들을 만들고 합친 이후에 하나의 struct learner를 만들고, 그 weight를 찾는 방식을 말한다.

Practical Gradient Descent Methods

Stochastic gradient Descent

• 하나의 샘플을 이용

Neural networks are computing systems vaguely inspired by the biological neural networks that constitute animal brains.

$$\begin{aligned} \frac{\partial \operatorname{loss}}{\partial w} &=\frac{\partial}{\partial w} \frac{1}{N} \sum_{i=1}^{N}\left(y_{i}-\hat{y}_{i}\right)^{2} \\ &=\frac{\partial}{\partial w} \frac{1}{N} \sum_{i=1}^{N}\left(y_{i}-w x_{i}-b\right)^{2} \\ &=-\frac{1}{N} \sum_{i=1}^{N}-2\left(y_{i}-w x_{i}-b\right) x_{i} \end{aligned}$$ $$\begin{aligned} &w \leftarrow w-\eta \frac{\partial \operatorname{loss}}{\partial w} \\ &b \leftarrow b-\eta \frac{\partial l o s s}{\partial b} \end{aligned}$$

시퀀스 데이터

• 소리, 문자열, 주가 등처럼 순차적으로 나타나는 데이터를 시퀀스 데이터로 분류한다.
• 독립동등분포(i.i.d.) 가정을 잘 위배하기 때문에 순서를 바꾸거나 과거 정보에 손실이 발생하면 데이터의 확률분포도 바뀌게 된다.

$$P(X_1, ..., X_t) = P(X_t \mid X_1, ..., X_{t-1})*P(X_1,...,X_{t-1})\\=\prod_{s=1}^{t}P\left(X_{S} \mid X_{S-1}, \ldots, X_{1}\right)$$

• 이전 시퀀스의 정보를 가지고 앞으로 발생할 데이터의 확률분포를 다루기 위해 조건부확률을 이용할 수 있다.

• 시퀀스 데이터를 다루기 위해선 길이가 가변적인 데이터를 다룰 수 있는 모델이 필요하다.

  

  $H_T = Net_\Theta(H_{t-1}, X_{t-1})$​

• 시퀀스 길이가 길어지면 BPTT를 통한 역전파 알고리즘의 계산이 불안정해지므로 길이를 끊는 것이 필요하다. (truncated BPTT)

• 이러한 문제들 때문에 Vanila RNN은 길이가 긴 시퀀스를 처리하는데 문제가 있다.

  • 이를 해결하기 위해 등장한 것이 LSTM과 GRU이다.

• 지금까지 배운 다층신경망(MLP) 구조는 각 뉴런들이 선형모델과 활성함수로 모두 연결된 (fully connected) 구조였다.
• Convolution 연산은 이와 달리 커널(kernel)을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조이다.
• Convolution 연산의 수학적 의미는 신호(signal)을 커널을 이용해 국소적으로 증폭 또는 감소시켜서 정보를 추출 또는 필터링하는 것이다.
• 커널은 정의역 내에서 움직여도 변하지 않고(translation invariant) 주어진 신호에 국소적(local)으로 적용한다.

2차원 Convolution 연산

• 커널을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조

• 입력크기를 (H, W), 커널 크기를 $(K_H, K_W)$, 출력 크기를 $(O_H, O_W)$ 라고 하면 출력 크기는 다음과 같이 계산한다.

  $$O_H = H - K_H + 1\\ O_W = W - K_W + 1$$

• 채널이 여러개인 2차원 입력의 경우 2차원 Convolution을 채널 개수만큼 적용한다. 텐서를 직육면체 블록으로 이해하면 좀 더 이해하기 쉬움.

• Convolution 연산은 커널이 모든 입력데이터에 공통으로 적용되기 때문에 역전파를 계산할 때도 convolution 연산이 나오게 된다.

조건부확률

• 

• 조건부확률 P(A | B)는 사건 B가 일어난 상황에서 사건 A가 발생할 확률을 의미한다.

• 베이즈 정리는 조건부확률을 이용하여 정보를 갱신하는 방법을 알려준다.

• 

• 

  • theta: 모수 (데이터가 관찰될 확률)

  • 사후확률: 데이터를 관찰했을 때 이 가설이 성립할 확률 (데이터 관측 이후 측정한 확률이라 사후확률임)

  • 사전확률: 모델링 이전에 사전에 주어진 확률로 이해할 것. (데이터 분석 전 타겟에 대한 모수나 가설 등 미리 설정한 값.)

  • 가능도: 현재 주어진 파라미터(모수)가정에서 이 데이터가 관찰될 확률

  • Evidence: 데이터 전체의 분포

  • ex) COVID-99의 발병률이 10%로 알려져있다. COVID-99에 실제로 걸렸을 때 검진될 확률은 99%, 실제 걸리지 않았을 때 오검진될 확률이 1%라고 할 때, 어떤 사람이 질병에 걸렸다는 결과가 나왔을 때 정말로 COVID-99에 감염되었을 확률은?

    • 사전확률, 민감도(Recall), 오탐율(False alarm)을 가지고 정밀도(Precision)을 구하는 문제임.

    • 사전확률 P(theta) = 10% = 0.1

    • 가능도 P(D given theta) = 99% = 0.99, 오탐율 = 1% = 0.01
    • evidence P(D) = sum(P(D given theta) P(theta)) = 0.99 0.1 + 0.01 * 0.9 = 0.108
    • So, P(theta given D) = 0.1 * (0.99 / 0.108) ~= 0.916

  • COVID-99 판정을 받은 사람이 두 번째 검진을 받았을 때도 양성이 나왔을 때, 진짜 COVID-99에 걸렸을 확률은?

    • 베이즈 정리를 통해 새로운 데이터가 들어왔을 때 앞서 계산한 사후확률을 사전확률로 사용하여 갱신된 사후확률을 계산할 수 있다.

• 조건부 확률은 유용한 통계적 해석을 제공하지만, 인과관계(Causality)를 추론할 때 함부로 사용해서는 안된다.

  • 인과관계는 데이터 분포의 변화에 강건한 예측모형을 만들 때 필요하다.
  • 인과관계를 알아내기 위해서는 중첩요인(confounding factor)의 효과를 제거하고 원인에 해당하는 변수만의 인과관계를 계산해야 한다. 제거하지 않았을 때는 가짜연관성(spurious correlation)이 나온다.

모수란?

• 통계적 모델링은 적절한 가정 위에서 확률분포를 추정(inference)하는 것이 목표이며, 기계학습과 통계학이 공통적으로 추구하는 목표이다.
• 유한한 개수의 데이터만 관찰해서 모집단의 분포를 정확하게 알아낸다는 것은 불가능하다. 때문에 근사적으로 확률분포를 추정할 수밖에 없다.
• 데이터가 특정 확률분포를 따른다고 선험적(a priori)으로 가정한 후 그 분포를 결정하는 모수(parameter)를 추정하는 방법을 모수적 방법론이라고 한다.
• 특정 확률분포를 가정하지 않고 데이터에 따라 모델의 구조 및 모수의 개수가 유연하게 바뀌면, 그것을 비모수(nonparametric) 방법론이라 부른다.
  • 기계학습의 많은 방법론은 비모수 방법론에 속한다.
  • 모수가 무한히 많거나 모수가 데이터에 따라 바뀌는 것이지, 비모수방법론에는 모수가 없다는 것이 아니다.

확률분포 가정하기(예제)

• 우선 히스토그램을 통해 모양을 관찰한다.
  1. 데이터가 2개의 값(0 또는 1)만 가지는 경우 -> 베르누이분포
  2. 데이터가 n개의 이산적인 값을 가지는 경우 -> 카테고리분포
  3. 데이터가 [0, 1]사이에서 값을 가지는 경우 -> 베타분포
  4. 데이터가 0 이상의 값을 가지는 경우 -> 감마분포, 로그정규분포 등
  5. 데이터가 R 전체에서 값을 가지는 경우 -> 정규분포, 라플라스분포 등

데이터로 모수 추정

• 데이터의 확률분포를 가정했다면, 모수를 추정해볼 수 있다.
• 정규분포의 모수는 평균과 분산으로, 이를 추정하는 통계량은 아래 식과 같다.
  • 
  • 표본분산을 구할 때 N이 아니라 N - 1 로 나누는 이유는 불편(unbiased) 추정량을 구하기 위해서다.
• 통계량의 확률분포를 표집분포(sampling distribution)라 부르며, 특히 표본평균의 표집분포는 N이 커질수록 (데이터가 많아질수록) 정규분포를 따르게 된다.
  • 이것을 중심극한정리라고 부르며, 모집단의 분포가 정규분포를 따르지 않아도 성립한다.

최대가능도 추정법

• 표본평균이나 표본분산은 중요한 통계량이지만 확률분포마다 사용하는 모수가 다르므로 적절한 통계량이 달라지게 된다.
• 이론적으로 가장 가능성이 높은 모수를 추정하는 방법 중 하나는 최대가능도 추정법(maximum likelihood estimation, MLE)이다.
• 데이터집합 X가 독립적으로 추출되었을 경우엔 로그가능도를 최적화한다.
  • 로그가능도를 사용하는 이유
    1. 로그가능도를 최적화하는 모수는 가능도를 최적화하는 MLE가 된다.
    2. 데이터의 숫자가 수억 단위가 된다면 컴퓨터의 정확도로는 가능도를 계산하는 것이 불가능해진다.
    3. 데이터가 독립일 경우, 로그를 사용하면 가능도의 곱셈을 로그가능도의 덧셈으로 바꿀 수 있기 때문에 컴퓨터로 연산이 가능해진다.
    4. 경사하강법으로 가능도를 최적화할 때 미분 연산을 사용하게 되는데, 로그가능도를 사용하면 연산량을 O(N^2)에서 선형시간으로 줄일 수 있다.
    5. 대개 손실함수의 경우 경사하강법을 사용하므로 음의 로그가능도(negative log-likelihood)를 최적화하게 된다.

딥러닝에서 확률론이 필요한 이유

• 딥러닝은 확률론 기반의 기계학습 이론에 바탕을 둔다.
• 손실함수 등의 작동원리가 데이터 공간을 통계적으로 해석해서 유도하기 때문.
• 회귀분석에서 손실함수로 사용되는 L2-노름은 예측오차의 분산을 가장 최소화하는 방향으로 학습
• 분류문제에서 사용되는 교차엔트로피(cross-entropy)는 모델 예측의 불확실성을 최소화하는 방향으로 학습
• 분산 및 불확실성을 최소화하기 위해서는 측정 방법을 알아야한다.

확률분포

• 확률분포란 데이터 공간에서 데이터를 추출하는 분포이다.
• 데이터는 확률변수로 (x, y) ~ D 라고 표기한다.
• 결합분포 P(x, y)는 D를 모델링한다.
  • D는 이론적으로 존재하는 확률분포이기 때문에 사전에 알 수 없다.

확률변수

이산확률변수

• 이산형 확률변수는 확률변수가 가질 수 있는 경우의 수를 모두 고려하여 확률을 더해서 모델링한다.

연속확률변수

• 연속형 확률변수는 데이터 공간에 정의된 확률변수의 밀도 위에서의 적분을 통해 모델링한다.
• 밀도함수는 누적확률분포의 변화율을 모델링한 것으로 확률로 해석해서는 안된다.

조건부확률과 기계학습